

Also an extension of a half synchronized system called weak. Here we give a counterexample to this in higher dimensions. Note that if X is a strongly irreducible subshift, this implies the (non-periodic) specification property. Fischer cover of an irreducible subshift is related to the dynamical properties of that system. Berthé, Valérie Ferenczi, Sébastien Mauduit, Christian Siegel, A. It is known that in one dimension an irreducible subshift of finite type has a unique measure of maximal entropy, the so-called Parry measure. David Damanik, Strictly Ergodic Subshifts and Associated Operators, (2005) A complete set of computable invariants is given for deciding whether two irreducible subshifts of finite type have topologically equivalent suspension.Some subshifts can be characterized by a transition matrix, as above such subshifts are then called subshifts of finite type.
#IRREDUCIBLE SUBSHIFT FULL#
Introduction to Dynamical Systems (2nd ed.). A subshift is then any subspace of the full shift that is shift-invariant (that is, a subspace that is invariant under the action of the shift operator), non-empty, and closed for the product topology defined below. Matthew Nicol and Karl Petersen, (2009) " Ergodic Theory: Basic Examples and Constructions",Įncyclopedia of Complexity and Systems Science, Springer We illustrate this correspondence by using the Potts model and a model of our own, inspired by the vertex models in statistical mechanics. For a subshift Z AG, we say Z is strongly irreducible iff iZ is. between a simplex of measures of maximal entropy of a strongly irreducible subshift of nite type and a simplex of equilibrium states of the corresponding statistical mechanics model. View on Springer Save to Library Create Alert On the density of periodic configurations in strongly irreducible subshifts T. We prove that the the Fischer automaton is a topological conjugacy invariant of the underlying irreducible sofic shift.Let V See also Some basic facts about strongly irreducible subshifts. A subshift X CA' is said to be A-irreducible if it satisfies the following condition: if (21 and (22 are two finite subsets of G such that (21 and (220 are. We prove that if X AG is a strongly irreducible subshift then X has the Myhill property, that is, every pre-injective cellular automaton : X X is surjective.
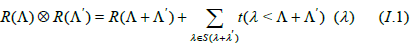
We characterize the Fischer automaton of an almost of finite type tree-shift and we design an algorithm to check whether a sofic tree-shift is almost of finite type. We show that for any subshift of finite type determined by an irreducible and aperiodic matrix. Thus Williams' conjecture is of greatest interest for irreducible matrices, especially primitive matrices. The topological dynamics and classification of irreducible SFTs easily reduce to the mixing case. It is a meaningful intermediate dynamical class in between irreducible finite type tree-shifts and irreducible sofic tree-shifts. This paper deals with chaos for subshifts of finite type. of finitely many irreducible SFTs, which support all the ergodic theory and recurrent dynamics, and a wandering set of connecting orbits.

We define the notion of almost of finite type tree-shift which are sofic tree-shifts accepted by a tree automaton which is both deterministic and co-deterministic with a finite delay.

We show that, contrary to shifts of infinite sequences, there is no unique reduced deterministic irreducible tree automaton accepting an irreducible sofic tree-shift, but that there is a unique synchronized one, called the Fischer automaton of the tree-shift. We introduce the notion of sofic tree-shifts which corresponds to symbolic dynamical systems of infinite ranked trees accepted by finite tree automata. Irreducible subshifts have unique measures of maximal entropy if they are for instance of finite type or sofic (factors of shifts of finite type).


 0 kommentar(er)
0 kommentar(er)
